2023 14 avril
Voir tous les articles
Comme autre exercice d’utilisation de ChatGPT 3.5 pour faire des choses étranges et voir ce qui se passe, j’ai décidé d’explorer une question intéressante : comment le temps nécessaire pour voyager d’un point A à un point B évolue-t-il avec la distance, dans le monde réel? Autrement dit, si vous effectuez un échantillonnage aléatoire à partir des endroits où se trouvent réellement les gens (par exemple, 56% des points que vous choisissez serait en ville) et vous utilisez les transports en commun, comment le temps de trajet s’adapte-t-il à la distance ?
Il est évident que la durée du trajet augmenterait plus lentement que linéairement : plus il faut aller loin, plus grandes sont les possibilités de recourir à des modes de transport plus rapides mais à coût fixe. Hormis quelques très rares cas chanceux, il n’existe pas de moyen pratique de prendre un bus pour aller plus vite si votre destination est à 170 mètres, mais si votre destination est à 170 mètres kilomètres loin, tout à coup, vous obtenez plus d’options. Et si c’est à 1 700 kilomètres, les avions arrivent.
J’ai donc demandé à ChatGPT les ingrédients dont j’aurais besoin :


Je suis allé avec le Ensemble de données GeoLife. J’ai remarqué que même s’il prétend couvrir des utilisateurs du monde entier, il semble se concentrer principalement sur les gens de Seattle et de Pékin, même s’ils visitent occasionnellement d’autres villes. Cela dit, je ne suis pas perfectionniste et ça me convenait. J’ai demandé à ChatGPT de m’écrire un script pour interpréter l’ensemble de données et extraire une coordonnée sélectionnée au hasard de chaque fichier :

Étonnamment, il Presque réussi du premier coup. Il a commis l’erreur de supposer que chaque élément de la liste était un nombre (values = [float(x) for x in line.strip().split(',')]), même si c’était peut-être en partie de ma faute : quand j’ai dit « les deux premiers valeurs» a probablement interprété cela comme impliquant que la ligne entière était composée de « valeurs » (c’est-à-dire de nombres).
J’ai corrigé le bug manuellement. Maintenant, j’ai un moyen d’obtenir des points sélectionnés au hasard où se trouvent les gens, et j’ai une API pour obtenir le temps de trajet en transports en commun entre les points.
Je lui ai demandé plus d’aide pour le codage :
- Demander comment obtenir une clé API pour l’API Google Maps Directions (a donné une réponse qui semble obsolète, mais a réussi à me diriger immédiatement vers le bon endroit)
- Écrire une fonction pour calculer la distance en ligne droite entre deux coordonnées GPS (a donné la bonne réponse du premier coup)
- Étant donné une liste de
(distance, time)paires, dessinant un nuage de points, avec le temps et la distance comme axes, les deux axes étant mis à l’échelle logarithmiquement (a donné la bonne réponse du premier coup) - Exécuter une régression linéaire sur les logarithmes de distance et de temps pour essayer d’ajuster les données à une loi de puissance (travaillé au premier essai, réussi au second)
Cela m’a donné des données vraiment intéressantes (elles sont filtrées pour des distances inférieures à 500 km, car au-dessus de 500 km, le meilleur itinéraire inclut presque certainement le vol et les directions Google Maps ne prennent pas en compte les vols) :
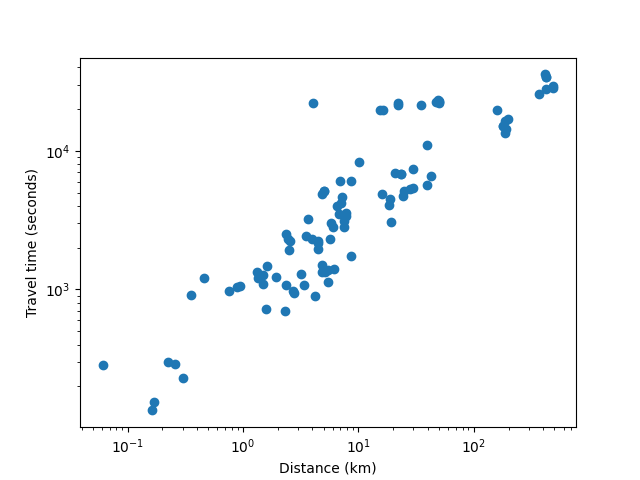
La loi de puissance donnée par régression linéaire est : travel_time = 965.8020738916074 * distance^0.6138556361612214 (temps en secondes, distance en km).
J’avais désormais besoin de données sur le temps de trajet pour des distances plus longues, où l’itinéraire optimal incluait les vols. Ici, les API n’ont pas pu m’aider : j’ai demandé à ChatGPT s’il existait des API capables de faire une telle chose, et cela n’a pas donné de réponse satisfaisante. J’ai eu recours à le faire manuellement :
- J’ai utilisé le même script, mais je l’ai légèrement modifié pour produire uniquement des paires de points qui étaient De plus distants les uns des autres de plus de 500 km.
- J’ai pris les 8 premiers résultats aux États-Unis et le top 8 avec au moins une extrémité en dehors des États-Unis, en sautant les résultats qui représentaient deux villes déjà couvertes.
- Pour chaque résultat que j’ai obtenu manuellement :
to_airport: temps de trajet en transports en commun depuis le point de départ jusqu’à l’aéroport le plus proche, en utilisant Google Maps hors de Chine et Cartes Baidu en Chine.from_airport: Le temps de trajet des transports en commun jusqu’au point final depuis l’aéroport le plus procheflight_time: Le temps de vol du point de départ au point d’arrivée. J’avais l’habitude de Vols Google) et j’ai toujours pris le résultat le plus haut, sauf dans les cas où le résultat le plus haut était complètement fou (plus de 2 fois la longueur du plus court), auquel cas j’ai pris le plus court.
- J’ai calculé le temps de trajet comme
(to_airport) * 1.5 + (90 if international else 60) + flight_time + from_airport. La première partie est une formule assez agressive (je suis personnellement beaucoup plus conservatrice que celle-ci) pour savoir quand partir pour l’aéroport : essayez d’arriver 60 minutes plus tôt si vous êtes national et 90 minutes plus tôt si vous êtes international, et multipliez le temps de trajet prévu par 1. , 5x en cas d’incident ou de retard.
C’était ennuyeux et je n’avais pas envie de perdre du temps à en faire plus de 16 ; Je suppose que si j’étais un chercheur sérieux, j’aurais déjà créé un compte TâcheLapin ou un service similaire qui permettrait d’embaucher plus facilement d’autres personnes pour le faire à ma place et obtenir beaucoup plus de données. De toute façon, 16 suffisent ; J’ai entré les données résultantes ici.
Enfin, juste pour m’amuser, j’ai ajouté quelques données sur le temps qu’il faudrait pour voyager vers différents endroits de l’espace : la lune (J’ai ajouté 12 heures au temps pour tenir compte du temps de trajet moyen d’une personne jusqu’au site de lancement), Mars, Pluton ET Alpha Centaures. Vous pouvez trouver mon code complet ici.
Voici le graphique obtenu :
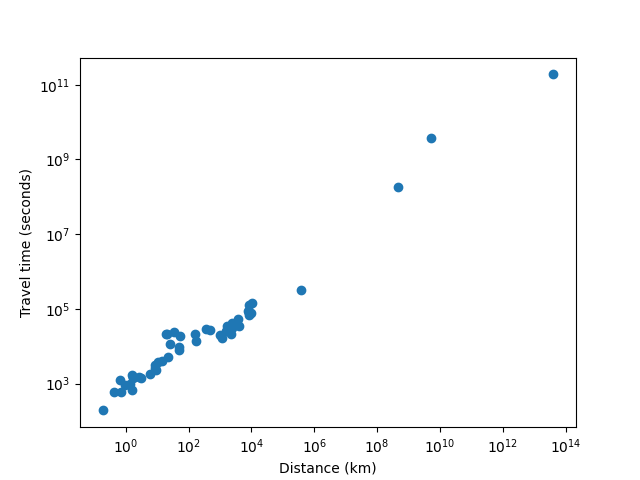
travel_time = 733.002223593754 * distance^0.591980777827876
WAAAAA ?!?!! D’après ce graphique, il semble qu’il existe une relation étonnamment précise qui régit le temps de trajet d’un point A à un point B et qui, d’une manière ou d’une autre, s’applique également à des modes de transport aussi radicalement différents que la marche, les métros et les bus, les avions et (!!) les véhicules, les vaisseaux spatiaux interplanétaires. et un vaisseau spatial interstellaire hypothétique. Je jure que je ne choisis pas la cerise sur le gâteau ; Je n’ai jeté aucune donnée gênante, tout ce que j’ai vérifié (y compris les éléments spatiaux) j’ai mis dans le graphique.
ChatGPT 3.5 a fonctionné extraordinairement bien cette fois-ci ; il a certainement trébuché et est tombé beaucoup moins que ma mésaventure précédente, où j’ai essayé d’obtenir de l’aide pour convertir les bafyhashs IPFS en hexadécimal. Dans l’ensemble, ChatGPT semble remarquablement efficace pour m’apprendre des bibliothèques et des API dont je n’avais jamais entendu parler auparavant mais que d’autres personnes utilisent tout le temps ; cela réduit la barrière à l’entrée entre amateurs et professionnels et cela nous semble une chose très positive.
Nous y sommes donc, il semble qu’il existe une sorte de loi fractale vraiment étrange du temps de trajet. Bien entendu, différentes technologies de transport pourraient modifier cette relation : si l’on remplace les transports publics par des voitures et les vols commerciaux par des jets privés, le temps de trajet devient un peu plus linéaire. Et une fois que nous aurons téléchargé nos esprits sur du matériel informatique, nous pourrons voyager vers Alpha Centauri dans des véhicules beaucoup plus fous comme Avion ultraléger propulsé par des voiles légères basées sur Terre) qui pourrait nous permettre d’aller n’importe où à une fraction significative de la vitesse de la lumière. Mais pour l’instant, il semble exister une relation étrangement cohérente qui rapproche le temps de la racine carrée de la distance.








